| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Fine-tuning
- glibcxx
- Mac
- gemma2
- ubuntu
- diffusion
- llm tuning
- lora+
- continued pre-training
- backbone
- prompt
- Text-to-Image
- instruct pre-training
- instruction tuning
- Lora
- full fine-tuning (fft)
- langchain
- error: mkl-service + intel(r)
- domain-adapted pre-training
- instruction tuning (it)
- PEFT
- instruct-pt
- continual pre-training
- sfttrainer
- transformer
- llm
- continued pre-train (cpt)
- CPT
- cross-document attention
- ViT
- Today
- Total
꾸준하게
[논문리뷰] Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise 본문
[논문리뷰] Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise
yeonsikc 2024. 5. 23. 19:05
arxiv 2022 Paper Code
Arpit Bansal, Eitan Borgnia, Hong-Min Chu, Jie S. Li, Hamid Kazemi, Furong Huang, Micah Goldblum, Jonas Geiping, Tom Goldstein
University of Maryland, New York University
19 Aug 2022

Abstract
일반적인 diffusion은 가우시안 노이즈를 넣어 열화시키고 이것을 복원하는 과정을 거친다. 저자는 실험을 통해 diffusion 모델의 생성 동작은 이미지 품질 저하 선택에 크게 의존하지 않는다는 것을 발견하였다. 다양한 결정론적 품질 저하(블러, 마스킹 등)을 사용하는 경우에도 diffusion 모델의 기반이 되는 학습 및 테스트 시간 업데이트 규칙을 쉽게 일반화하여 생성 모델을 생성할 수 있다고 주장한다.
Introduction
이전 연구에서는 학습 및 생성 시 가우시안 노이즈를 이용하는 것이 일반적이었다. 본 연구에서는 이러한 것에 의문을 갖고 diffusion 모델이 작동하는데에 있어 가우시안 노이즈나 랜덤성이 필요한지를 조사하였다. 저자는 랜덤성이 없는 블러, 다운샘플링과 같은 기법들에 간단한 loss를 사용하여 일명 cold diffusion이라는 랜덤성 없는 모델을 만들었다.
Generalized Diffusion
Model Components and training
이미지 $x_0 \in \mathbb{R}^N$와 오퍼레이터(Diffusion 모델) $D$, timestep $t$가 주어졌을 때, $x_t = D(x_0, t)$이다. 열화된 출력 분포 $D(x_0, t)$는 연속적으로 변화해야 하며 다음 조건을 만족해야한다.
$$D(x_0, 0) = x_0$$
저자는 여기에서의 $D$를 기존의 가우시안 노이즈가 아닌 방법들을 적용하고자 하였으며, $D$를 정의함에 있어 자연스레 이를 복원하는 $R$ 또한 정의해야 했으며 이는 아래의 조건을 만족해야한다.
$$R(X_t, t) \approx x_0$$
실제로 위 연산자는 $\theta$에 의해 파라미터화 된 신경망을 통해 구현된다. 복원 네트워크는 다음 최소화 문제를 통해 학습된다.
$$ \min\limits_{\theta} \mathbb{E}_{x \sim X} || R_{\theta}(D(x, t), t) - x || \tag{1} $$
- $x$ : distribution $X$에서의 랜덤 이미지 샘플
- $|| \cdot ||$ : l1 norm
Sampling from the model



위 Algorithm 1은 노이즈 이미지를 one-step으로 복원하고 복원된 이미지로 다시 노이즈 이미지(방금 복원전의 이미지보다 t-1 timestep을 복원)로 열화하는 프로세스이다. 즉, $R(D(X_0, t),t) = x_0\ \forall t$. 그러나 이 알고리즘은 $x_s$에 계속 오차가 축적되어 $D(x_0,s)$에서 멀어지게 되고, 부정확한 재구성이 발생할 수 있다. 하지만 이는 노이즈 기반 diffusion에서는 잘 작동하는데, 이는 복원 연산자가 입력의 (무작위 가우시안) 오류를 수정하도록 학습되었기 때문일 수 있다고 저자는 주장하였다.
저자는 Algorithm 2를 통해 이를 해결한 방법을 제안한다. 바로 예측 오차를 식에 포함하는 것. 위 그림에서 볼 수 있듯이 Algorithm 1의 경우, deblurring 모델에서 보여진 바와 같이 smooth/differentiable 열화를 가진 cold diffusion에서 좋지 않은 결과를 보였다. 하지만 Algorithm 2를 이용하여 이를 해소한 것을 볼 수 있다.
Properties of Algorithm 2
복원 연산자가 열와 연산자의 완벽한 역수인 경우, Algorithm 1, 2 모두 $x_s = D(X_0,x) \forall{s<t}$에 대해 완벽하게 재구성하는 것을 알 수 있다. 저자는 이 알고리즘의 안정성에 대해 분석하였다. Algorithm 2의 식에서 $D(x,s) \approx x\ + \ s\cdot e$ 형태의 선형 열화 함수를 갖는 모델이라고 가정하였을 때, 다음과 같은 수식 전개가 가능해진다.

위 식을 보면 알 수 있듯이, $R$에 관계없이 $x_s = D(X_0, s) for all s < t$가 성립한다. 다른말로, 어느 $R$을 선택하더라도 반복은 $R$이 열화모델 $D$에 대하여 완벽한 역을 가질 때와 동일하게 동작한다. 그렇지만 Algorithm 1에서는 이것이 성립하지 않는다. ($x_0 \neq D(R(x,0), 0) = R(x,0)$)
Generalized Diffusions with Various Transformations
저자는 다음 태스크와 데이터 셋에 대한 실험을 진행하였다.
- Task : deblurring, inpainting, super-resolution, snow removal
- Dataset : MNIST, CIFAR-10, CelebA
Deblurring
$$x_t = G_t * x_{t-1} = G_t * \ldots * G_1 * x_0 = \bar{G}_t * x_0 = D(x_0, t) \tag{2}$$
- $G_t$ : 가우시안 커널
- $*$ : convolution operator (blur)
저자는 위에서 언급한 식(1)의 loss를 최소화하는 방향으로 모델을 학습하였으며 Algorithm 2과 DNN을 사용하여 이미지를 복원하였다.


실험 결과, RMSE나 SSIM에서 저자가 제안하는 방식이 기존보다 성능이 안좋게 나왔지만 FID score에서는 좋게 나왔다. 낮은 FID score와 질적으로 개선되어 보이는 이 결과는 학습된 분포를 실제 데이터 다양체에 더 가깝게 만드는 일반화된 샘플링 루틴의 이점을 보여준다고 저자는 주장하였다.
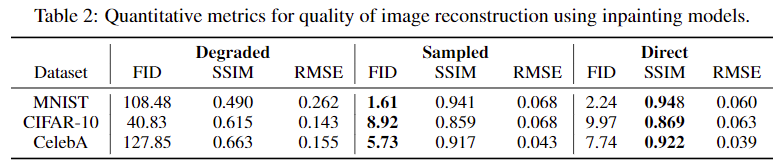
Inpainting
저자는 인페인팅 실험을 위해 이미지 임의의 공간에 점점 옅어지는 회색 원을 입히는 것으로 열화하였다. 세부적으로, $n \times x$ 크기의 이미지에 대해 $\beta$ 분산을 갖는 2D 가우시안 커브를 적용한다. 그 후, 곡선의 정점이 1이 되도록 정규화하고 1에서 결과를 빼서 마스크의 중심이 0이 되도록 하였다. MNIST와 CIFAR-10에서는 랜덤한 위치에 적용하였으나 CelebA에서는 중앙을 선택하였다. 최종 마스크는 $z_\beta$로 표기하였다.
입력 이미지 $x_0$은 timestep $T$에 따라 점차 증가하는 $\beta_i$의 마스크 $z_{\beta_i}$를 점진적으로 적용하였다. 이때, 파라미터 $\beta_i$를 조정하여 각 스텝마다 제거될 정도를 제어할 수 있다. 이에 대한 수식은 $D(x_0, t) = x_0 \cdot \prod_{i=1}^t z_{\beta_i}$이며 연산자 $\cdot$은 entry-wise multiplication(각 요소별 곱셈)이다. 아래 그림과 표를 보아 블러와 비슷한 결과임을 알 수 있다.

Super-Resolution
이 작업에서는 열화 연산자 $D$가 2배수의 Downsample을 적용한다. 최종적으로 열화된 해상도는 MNIST와 CIFAR-10는 $4 \times 4$, Celeb-A는 $2 \times 2$이 되게 된다. 각 down-sampling 후에는 원본 사이즈로 Resize를 적용한다(nearest-neighbor interpolation 적용). 결과 그림과 표를 보면 좋은 결과로 보여지진 않는다.


Snowification
저자는 전통적인 열화와는 별도로 ImageNet-C에서 눈(Snow) 변환의 official implementation를 통해 합성 눈 제거 작업에 대한 결과를 추가로 보인다. 이 실험의 목적은 일반적인 Diffusion이 이국적인 변환으로도 성공할 수 있음을 확인한다.
아래 결과를 보면 snow 효과를 적게 적용한 CIFAR-10이나 많이 적용한 Celeb-A 모두에서 좋은 복원력을 볼 수 있었다.


Cold Generation
Image generation using blur
저자는 블러 열화 적용 시, 각 이미지에 $27 \times 27$ 크기의 가우시안 커널로 300 step 이상의 process를 적용했다고 한다. 이때 표준편차는 1에서부터 0.01까지 기하급수적(exponential)으로 감소하도록 하였으며 channel별 평균(channel-wise means)을 갖는 분포를 통해 간단한 GMM(Gaussian mixture model)을 fit했으며, 스크래치로부터 이미지 생성을 위해 GMM에서 채널별 샘플링하고, 3D-vector를 3개의 채널을 가진 $128 \times 128$ 이미지로 확장한 다음 Algorithm 2를 적용하였다고 한다.
아래 표와 그림은 기존 Noise-based diffusion(Hot Diffusion)과 blur를 이용한 cold diffusion에 대한 결과이다. 표를 보면, 위에서 제안한 파이프라인은 충실도는 높지만 다양성이 낮은 이미지를 생성하며 이는 channel-wise means GMM에서 샘플링된 $x_T$의 픽셀 간에 완벽한 상관관계에 기인하는 것으로 나타났다. 픽셀간의 대칭을 깨기 위해 샘플링된 각 $x_T$에 소량의 가우시안 노이즈($sd\ = \ 0.002$를 추가하는 트릭을 적용하였으며 이는 생성된 이미지의 품질을 크게 향상시킬 수 있었다.(CelebA 기준 97.00 -> 49.45)

Conclusion
기존의 Diffusion 모델들은 forward와 reverse 프로세스 모두 가우시안 노이즈에 의존한 것과 달리, 저자는 diffusion 모델에 랜덤 노이즈를 완전 제거해도 가능하다는 것을 입증하였으며 임의의 변환 방법을 제안하였다. 이로인해 블러, 인페인팅 및 다운 샘플링과 같은 결정론적 정하로 인해 영향을 받는 이미지를 복원할 수 있게 되었다. 이러한 방법들은 이미지 생성 및 그 이상을 포함하는 다양한 응용들에 유용한 것으로 증명될 수 있다고한다.




